|
|
Soalan berkaitan Matematik & Matematik Tambahan
[Copy link]
|
|
|
Originally posted by 6630 at 22-8-2005 01:25 PM
Azlan ialah seorang murid yang baru berpindah dari SMK Terengganu ke sekolah ini selepas ujian pertama telah diadakan.Dia hanya mengambil 3 ujian Matematik Tambahan sahaja dan memperoleh markah min ...
ko cuba guna EXCEL.... use this formula
A B C
1 Markah Min Azlan Deduksi
2 0 =(min(63*3 + A2)/4) = if(B1>64,"Markah Azlan > Markah Salina","Markah Azlan < Markah Salina").
3 1
4 2
5 3
6 4
.
.
.
.
.
. 100 |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by adlismel at 24-8-2005 09:52 AM
ko cuba guna EXCEL.... use this formula
A B C
1 Markah Min Azlan Deduksi
2 0 ...
jap...utk strategi kedua tu pakai excel ke? kiranya utk strategi pertama guna kalkulator
then for strategy kedua guna excel? mcm tu ke?
saya pun memula buat camtu gak, then semak ngan kawan strategi dia lain pula. |
|
|
|
|
|
|
|
|
|
|
|
Azlan ialah seorang murid yang baru berpindah dari SMK Terengganu ke sekolah ini selepas ujian pertama telah diadakan.Dia hanya mengambil 3 ujian Matematik Tambahan sahaja dan memperoleh markah min 62.Satu lagi ujian Matematik Tambahanakan diadakan.Azlan akan mengambilnya sebagai ujian keempat dan Salina pula akan mengambilnya sebagai ujian kelima dan min 4 ujian sebelumnya ialah 64. Cari semua markah yang perlu dicapai oleh Azlan dalam integer bagi ujian ini supaya markah minnya melebihi markah min Salina.
Terangkan bagaimana memperoleh penyelesaian dengan menggunakan sekurang-kurangnya dua strategi.
dalam soalan ni diberi gunakan min salina bagi ujian keempat ialah 64. Uji markah salina dari 0 hingga 100.
so, utk penyelesaian soalan ni, perlu gunakan min salina utk ujian kelima atau ujian keempat utk dibandingkan ngan markah min azlan supaya melebihi markah min salina?
sy nak minta kepastian sbb utk strategi pertama sy uji markah salina dan azlan menggunakan rumus ni :
utk salina  256 + x ) / 5 256 + x ) / 5
utk azlan : ( 186 + x ) /4
di mana x= markah ujian dari 0-100
utk strategi kedua sy gunakan ketaksamaan linear. tapi betul ke rumus tu? |
|
|
|
|
|
|
|
|
|
|
|
well, since aku takde mase sangat, aku akan try kasi clue bile aku ade masa. let me start with part a).
Soklan killerno7 dari thread Tugasan Kerja Projek Matematik Tambahan 2005,help me out pls !
Salina ialah seorang murid SMK Perak . Dia telah mengambil ujian Matematik Tambahan sebanyak 4 kali dari bulan Julai bagi thaun 2005 .
(a) Markah min yang diperoleh oleh Salina bagi empat ujian itu ialah 64 . Berapakah markah yang perlu dicapai oleh Salina dalam ujian kelima untuk mendapat markah min 70 ?
(b) Jika markah min Salina bagi empat ujian itu ialah m dan markah minnya bagi lima ujian itu ialah n , ungkapkan markah Salina bagi lima ujian itu sekurang-kurangnya 4/5 daripada markah minnya bagi empat ujian sebelumnya .
(c) Azlan ialah seorang murid yang baru berpindah dari SMK Terengganu ke sekolah ini selepas ujian pertama telah diadakan . Dia hanya mengambil 3 ujian Matematik Tambahan sahaja dan memperoleh markah min 62 . Satu lagi ujian Matematik Tambahan akan diadakan . Azlan akan mengambilnya sebagai ujian keempat dan Salina pula akan mengambilnya sebagai ujian kelima .
(i) Jadualkan semua markah yang perlu dicapai oleh Azlan dalam bentuk integer bagi ujian ini supaya markah minnya melebihi markah min Salina . Uji markah Salina dari 0 hingga 100 dan gunakan markah min Salina bagi empat ujian itu sebagai 64 . Terangkan bagaimana anda memperoleh penyelesaian dengan menggunakan sekurang-kurangnya dua strategi .
(ii) Jika Salina mendapat markah 80 , nyatakan julat markah yang perlu diperoleh oleh Azlan untuk mengatasi markah Salina .
Soalan Lanjutan
1. Bagi kes di mana markah min Azlan lebih daripada markah min Salina , teroka kemungkinan sama ada markah Azlan bagi keeempat kurang daripada markah Salina bagi ujian kelima .
2. Bagi kes di mana markah min Azlan kurang daripada markah min Salina , teroka kemungkinan sama ada markah Azlan bagi ujian keempat lebih daripda markah Salina bagi ujian kelima .
part a)
markah min asal,
min_1 = 64
bilangan exam asal,
n_1=4
markah min yang dia nak
min_2 =70 for n_2=5
min = total / n
so, min_1 = total_1 / n_1, maka total_1 = min_1 * n_1 = exam_1 + exam_2 + exam_3 + exam_4
total_2 mestilah total_1 tambah exam ke lima
so
total_2 = total_1 + exam_5
exam_5 = total_2 - total_1
cuba cari total_2, pastu gunakan utk dapatkan exam_5. dah dapat jawapan sila post kat sini, leh check.
p/s: banyak sangat ke clue yang aku bagi? |
|
|
|
|
|
|
|
|
|
|
|
Min = Σx / N
Σx / 4 = 64
Σx = 64 x 4 = 256
Min baru = 70,
Σx / 5 = 70
Σx = 70 x 5 = 350
Maka markah yg perlu dicapai olh salina,
350 |
|
|
|
|
|
|
|
|
|
|
|
Soalan (b)
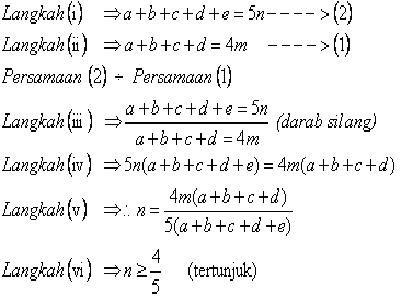 |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by adlismel at 6-9-2005 10:06 AM
Soalan (b)
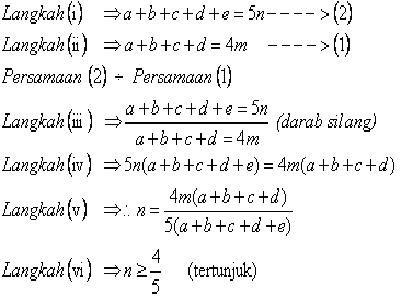
Silap. (Langkah iv). Anda sepatutnya menunjukkan n >= 4m / 5. |
|
|
|
|
|
|
|
|
|
|
|
|
betul ler.. aku terlupa m tu heee sollly |
|
|
|
|
|
|
|
|
|
deepjunior This user has been deleted
|
Please help me on this one.
If a point moves along a line so that its distance s (in feet) from 0 is given by s = t + t cos^2 t at time t seconds, find its instantenous velocity at t = 3 |
|
|
|
|
|
|
|
|
|
|
|
the equation is not dimensionally homogeneous.
because
s has the unit of length, and t has the unit of time
s= t + t*(cos t)^2
length = time + (time * (dimentionless quantity)^2 ) <---product of sine cosine etc is dimentionless
length = time <--see, contradiction here.
so, kalo jumpe atau derive ape ape equation, check dimension dulu. kalo dimension tak kena, kompom equation tu salah.
kalo ade version equation tu yang lebh lengkap, sila type balik. |
|
|
|
|
|
|
|
|
|
|
|
lagi satu, argument utk cos , iaitu t cam tak kena jek. usually unit argument utk trigonometric function ialah angle.
mungkin bukan cos t kot? mungkin cos wt, where w has the unit of rad/s <-angular velocity. |
|
|
|
|
|
|
|
|
|
deepjunior This user has been deleted
|
|
nope. the equation is right. The only thing that I didn't mention is they ask me to use a graphic calculator. |
|
|
|
|
|
|
|
|
|
|
|
or does the question look like this
s = 1t .....
where 1 before t has the unit of velocity (length/time)? otherwise it can't be right. an equation should have the same dimension on both sides, otherwise it's not an equation because both sides are not equal. |
|
|
|
|
|
|
|
|
|
|
|
and yeah, you can get the derivative of s = t + t cos^2 t
s' =ds/dt = v = 1 + (cos t)^2 - 2t sin t cos t
by hand, graphing calculator or computer. but that still doesn't mean that the equation itself is corect. |
|
|
|
|
|
|
|
|
|
candy This user has been deleted
|
Originally posted by deepjunior at 20-10-2005 12:53 AM
nope. the equation is right. The only thing that I didn't mention is they ask me to use a graphic calculator.
Is your question " complete " ? Well , BeanDiesel mentioned before that the equation is not dimensionly homogenous ,
but if you insist that it is " correct " , then just differentiate it and substitute t=3 into it .
But somehow , sin (3 sec) seems abit weird as for "sin x" , we always have "x" without unit (not to mention the unit " angle " though) . |
|
|
|
|
|
|
|
|
|
deepjunior This user has been deleted
|
alright lets move on, next question, just for fun
Air is being pumped into a spherical balloon at a constant rate of 3 cubic centimeters per second. How fast is the radius of the balloon changing when the volume is 60 cubic centimeters? |
|
|
|
|
|
|
|
|
|
|
|
dv/dt = known, 3 cubic cm/s (1)
assuming that the baloon is a sphere, v=4*pi*r^3/3, rearrange to get r as a function of v
r = cubicroot( 3v/(4*pi) )
get the derivative of r, r' = dr/dv
substitute in ----> dr/dt = dv/dt * dr/dv , plug in V=60 cubic cm
note: we are assuming that the density of the air does not change. |
|
|
|
|
|
|
|
|
|
candy This user has been deleted
|
|
How many digits are there in 8^112 x 5^330 ? (without using calculator) |
|
|
|
|
|
|
|
|
|
|
|
hi
f : x --> -x^2 + 3x + 6
find the values of x when f(x) = 2x
:bgrin: |
|
|
|
|
|
|
|
|
|
|
|
Originally posted by Robab at 3/26/06 03:27 AM
f : x --> -x^2 + 3x + 6
find the values of x when f(x) = 2x
:bgrin:
i'm not familiar with the notation 'f:x'. f:x tu f as a function of x ke? like f(x)?
let's say it's f(x)=-x^2 + 3x + 6
you wanna find the values of x when f(x)=2x
so, -x^2 + 3x + 6 = 2x
x^2 - x - 6 = 0
now factorize it,
= (x-3) (x+2)=0
so, x= 3 or -2 <---jawapan
test
f(3) = -(3^2) + 3(3) + 6 = 6 = 2(3) .....ok
f(-2) = - (-2^2) + 3(-2) + 6 = -4 = 2(-2) .....ok |
|
|
|
|
|
|
|
|
|
| |
Category: Belia & Informasi
|